Ap Calculus Derivatives Of Inverse Functions Worksheet
ADVERTISEMENT
AP Calculus
Name ________________________________
CHAPTER 7 WORKSHEET
INVERSE FUNCTIONS
Seat # ______ Date ____________________
Derivatives of Inverse Functions
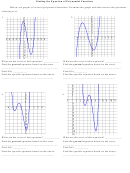
In 1-3, use the derivative to determine whether the function is strictly monotonic on its entire domain
and therefore has an inverse.
4
x
3
3
2
2.
3.
h
x
2
x
x
1.
f
x
2
x
g
x
x
a
b
4
Think About It…Find the derivative of
4.
. Notice that the subject derivative has the same
y
tan
x
sign for all values of x, so
y
tan
x
is a monotonic function. However,
y
tan
x
is not a one-
to-one function. Why?
In 5-6, (a) “delete” part of the graph of the function shown so that the part that remains is one-to-one.
Then, (b) find the inverse of the remaining part and (c) state its domain. (Note: there is more than one
correct answer for these questions!)
x
x
2
5.
6.
g
x
5
f
x
3
In 7-9, find the derivative of the inverse function at the corresponding value.
d
3
1
7.
Given
f
(
x
)
x
2
x
1
, find
f
(Note: you may need to use guess and check to solve an
dx
x
2
equation involved in this problem.)
d
5
3
1
8.
Given
g
(
x
)
2
x
x
1
, find
g
dx
x
1
π
π
d
1
9.
Given
h
(
x
)
sin
x
on the interval
,
find
h
2
2
dx
x
1
2
SEE OTHER SIDE
ADVERTISEMENT
0 votes
Related Articles
Related forms
Related Categories
Parent category: Education
 1
1 2
2 3
3 4
4