Ap Statistics Solutions To Packet 6 - Probability The Study Of Randomness Worksheet With Answers Page 13
ADVERTISEMENT
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
216.48 WINNING CONTRACTS Consolidated Builders has bid on two large construction projects.
The company president believes that the probability of winning the first contract (event A) is 0.6, that
the probability of winning the second (event B) is 0.4, and that the joint probability of winning both
jobs (event {A and B}) is 0.2. What is the probability of the event (A or B) that Consolidated will win
at least one of the jobs?
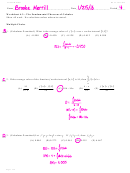
P(A or B) = P(A) + P(B) − P(A and B) = 0.6 + 0.4 − 0.2 = 0.8.
6.50 Draw a Venn diagram that illustrates the relation between events A and B in the preceding
C
C
exercise. Write each of the following events in terms of A, B, A
, and B
. Indicate the events on your
diagram and use the information in the exercise above to calculate the probability of each.
(a) Consolidated wins both jobs.
This event is {A and B}; P(A and B) = 0.2 (given).
C
(b) Consolidated wins the first job but not the second.
This is {A and B
}
C
) = P(A) − P(A and B) = 0.4.
P(A and B
C
(c) Consolidated does not win the first job but does win the second.
This is {A
and B}
C
and B) = P(B) − P(A and B) = 0.2.
P(A
C
C
(d) Consolidated does not win either job.
This is {A
and B
}
C
C
P(A
and B
) = 0.2 (so that the probabilities add to 1).
13
ADVERTISEMENT
0 votes
Related Articles
Related forms
Related Categories
Parent category: Education