Linear And Quadratic Functions Worksheet With Answers printable pdf download

Linear And Quadratic Functions Worksheet With Answers

Chapter 4

Linear and Quadratic Functions

Section summaries

Section 4.1 Linear Functions and Their Properties

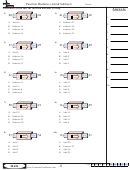
A linear function is one of the form

f (x) = mx + b ,

where m gives the slope of its graph, and b gives the y-intercept of its graph. The slope m

measures the rate of growth of the function, so a linear function is increasing if m > 0 and

decreasing if m < 0.

Review problems: p284 #17,21,25,37,43,49

Section 4.2 Building Linear Functions from Data

In this section linear functions are constructed from data presented in various ways.

Review problems: p290 #3,5,7,15,19,21

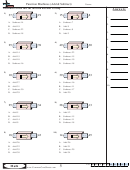
Section 4.3 Quadratic Functions and Their Properties

The general form of a quadratic function is

f (x) = a(x

+ k ,

where (h, k) is the vertex of the graph (which is a parabola). You can see from the formula

that h gives the left/right shift while k gives the up/down shift. The coeﬃcient a represents

a vertical stretch or compression. Since the basic member of this family is f (x) = x

, whose

graph opens up, the graph of f (x) = a(x

+ k will open up if a is positive, and down

if a is negative. If the graph opens up, its height is minimum at the vertex; if the graph

opens down, its height is maximum at the vertex.

Linear And Quadratic Functions Worksheet With Answers