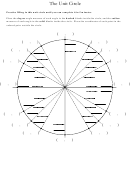
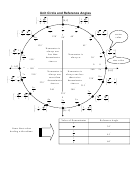
The Unit Circle And Exact Value Worksheet Template printable pdf download

The Unit Circle And Exact Value Worksheet Template

Unit # 6 – The Unit Circle and Exact Value

- unit circle → a circle with a ___________ centered at the _________ and has equation _____________

• terminal point → _____________________

• reference number → __________________

• cosine function → _____________________

• sine function → ____________________

Refer to TRIG CHART / UNIT CIRCLE SHEET to label parts of the Unit Circle:

1.) Complete the TRIG CHART → Use the 45 – 45 – right ∆ and the 30 – 60 – right ∆

For quadrant angles (0° and 90°), use your calculator

(Make sure to rationalize the denominator → EXAMPLE:

)

⋅

2.) Label the degree measure ABOVE each pt on the Unit Circle (only use increments of 30°, 45°, 60°)

3.) Draw diagonal lines through pairs of points that have the same reference number (angle):

a.) 30° and 210°

b.) 45° and 225°

c.) 60° and 240°

Ref Angle

150° and 330°

135° and 315°

120° and 300°

= 30°

= 45°

= 60°

4.) Label the terminal point (x , y) of each degree measure → (x = cos θ , y = sin θ)

5.) Also add the following to your sheet: Quadrant #’s and where sin, cos, tan are positive and negative.

Steps to Find Exact Value of an Angle: Some answers contain radicals (NO decimal answers)

1.) Find the reference angle B – Use the “Coloring Coding key” to help determine this.

2.) Use Trig Chart to look up value using reference angle B.

3.) Use “Signs” Diagram of Trigonometric Functions to determine if value is positive or negative

* If finding the exact value of a quadrant angle (90°, 180°, 270°, or 360°) → use values in terminal points

Examples: Using your TC/UC Sheet, find the exact value. Remember – NO DECIMALS!!!!

1.) sin 135° = _______

2.) cos 210° = _______

3.) cos 360° = _______

4.) tan – 780° = ______

5.) sin 390° = _______

6.) tan 270° = _______

7.) tan 150° = _______

8.) cos 315° = _______

9.) tan 210 ° = _______ 10.) cos 120°= _______

11.) sin – 540° = ____

12.) tan 675° = _____

The Unit Circle And Exact Value Worksheet Template